«Выдумают, надо же!.. Мир круглый! По мне хоть квадратный, а умов не мути!..», «От грамоты, от грамоты все идет, братья! Не в деньгах, мол, счастье, мужик, мол, тоже человек, дальше – больше, оскорбительные стишки, а там и бунт…», «Всех их на кол, братья!.. Я бы делал что? Я бы прямо спрашивал: грамотный? На кол тебя! Стишки пишешь? На кол! Таблицы знаешь? На кол, слишком много знаешь!»

(с) Трудно быть богом.

Я со студенческих времён люблю всяческие головоломки и каверзные задачи.

Но есть класс задач, которые я просто ненавижу. К этому классу задач относятся задачи, которые любят использовать психологи в своих дурацких тестах, якобы, на уровень интеллекта. Как правило, эти задачи сочиняют люди, считающие себя очень умными для выявления себе подобных.

Например, к подобным задачам относятся всякие задания типа "найди лишний предмет" или "дорисуй недостающую фигуру". Авторы задачи, как правило, оперируют какой-то своей логикой подбора фигур или предметов и почему-то считают, что другие люди должны думать и действовать так же. Хотя признаков "общности" и "лишнести" может быть несколько и для того, чтобы выбрать правильный ответ, надо встать на уровень дебилизма автора задачи.

Таких задач здесь не будет. Более того, все задачи, которые я публикую, имеют строгое и однозначное решение. Я постарался подобрать только такие задачки, для решения которых надо приложить "мозговое усилие". У некоторых решение возникает почти мгновенно, другим нужно время "на подумать".

К сожалению, в эпоху интернета решение абсолютного большинства задач можно найти в сети за пару минут. Именно поэтому я подобные задачки задаю друзьям во время походов, когда нет не то что интернета, но и вообще никакой связи с внешним миром, зато есть время посидеть вечером у костра и почертить прутиком на песке...

Мы с приятелями собирали эти задачки несколько лет. Жалко было бы их потерять, поэтому соберу их здесь.

Все задачки разделены на 4 категории. 1 - разминочные, 2 - простые, 3 - сложные, 4 - очень сложные. Многие задачки в том или ином виде есть в знаментых книжках Я.И.Перельмана.

Поехали.

1. Про концентрации

Имеется стакан с водой.
Имеется стакан с молоком.
(одинаковый объем)

Из стакана с водой одна чайная ложка воды переливается в стакан с молоком. Затем из стакана с молоком одна чайная ложка молока (с примесью воды) переливается обратно в стакан с водой.

Вопрос: В каком стакане % (концентрация) основного содержимого больше?

2. Задачка от Д'Артаньяна

Допустим, что если человек не ест 10 дней, то он умирает.
Допустим, что если человек не спит 10 дней, то он умирает.
Есть и спать одновременно он не может.
На исходе 10-е сутки, как он поел и поспал.

Что ему нужно сделать в первую очередь, чтобы не умереть.

3. Про черепашек (с олимпиады)

Имеем на плоскости квадрат со стороной a. В углах квадрата находятся черепахи, которых мы пронумеруем "по кругу" от 1-й до 4-й.
В некоторый момент времени T₀ черепахи начинают ползти с постоянной скоростью V.
Ползут они так, что в каждый момент 1-я черепаха ползёт по направлению к 4-й, 2-я черепаха - по направлению к 1-й, 3-я черепаха - по направлению к 2-й, 4-я черепаха - по направлению к 3-й.
Очевидно, что через какое-то время они встретятся. Каково это время?

4. Детская задача

Есть 20 металлических шариков. Нужно разложить их в два целлофановых пакета так, чтобы в одном пакете было ровно в два раза больше шариков, чем в другом. Резать шарики нельзя.

5. Простейшая

В камере сидят трое узников. Все разного роста - высокий, средний, низенький.
Есть напильник, чтобы перепилить решетку, но она находится высоко.
Встают пирамидкой - средний поднимается на высокого, затем на них влезает низкий. Но до решетки не достают всего несколько сантиметров.
Никаких предметов, на которые можно встать, нет.
Как им выпилить решетку?

6. Ещё детская

Кирпич весит килограмм и полкирпича. Сколько весит кирпич?

7. Про термостаты

В термостатах одинаковые анизотропные шары. Один лежит на абсолютно теплоизолирующей подставке, второй висит на абсолютно теплоизолирующей нити. За одинаковое время к шарам подводится одинаковое количество теплоты. Какой нагреется больше?

8. Простейшая географическая

Предположим, что мы вышли из Москвы и движемся строго на северо-восток.
Куда мы, в итоге, придём?

9. Продолжение географической задачи

Стоим мы на Северном полюсе. Вокруг ни севера, ни запада, ни востока, один сплошной юг.
И наблюдаем мы восход солнца.
Солнце взошло, допустим, на долготе Благовещенска.
Вопрос: на какой долготе солнце взойдёт в следующий раз?

10. Про взвешивание. Сложная

Знаю всего тёх человек, которые решили эту задачку.

Есть 12 монет. Известно, что одна из них фальшивая. Фальшивая монета отличается по весу.
Есть обычные рычажные весы с двумя чашками.
Найти фальшивую монету, произведя 3 (Три!) взвешивания.

11. Задачка с олимпиады

На плоскости 17 точек. Никакие три из них не лежат на одной прямой. Каждая точка соединена со всеми остальными отрезками прямой красного, синего или зелёного цвета.

Доказать, что в любом случае найдётся треугольник со сторонами одного цвета.

12. Геометрическая. Очень сложная.

13. Опять про взвешивание. Простая.

У нас 10 мешков с монетами. Настоящие монеты весят... ну пусть 10 грамм. В каком то мешке все монеты фальшивые. Фальшивые монеты тяжелее настоящих на 1 грамм. Количество монет в мешках неодинаково.
Весы как и в предыдущей задачке - рычажные с гирьками. Минимальная гирька - 1 грамм.
Как с помощью одного взвешивания определить мешок с фальшивыми монетами.

14. "Ковбойская" задача

Два пастуха год пасли в горах овец, и вот пришло время продавать свою отару. За каждую овцу они просили столько долларов, сколько изначально было овец в отаре. Когда всех овец продали, стали делить деньги по-ковбойски: 10$ — первому, 10$ — второму и так по очереди. Но тому, кто брал вторым, последняя десятка досталась неполной (т.е. ему осталось меньше 10$). Желая быть честным, тот, кто брал первым, отдал ему свой нож. Сколько стоил нож?

15. Задача про канадских лесорубов

Три канадских лесоруба пошли валить лес.
Поработав, сели перекусить.
Первый достал три пирога, второй достал пять пирогов. У третьего ничего с собой на перекус не было.
Все трое поделив еду поровну, поели. Но так как третий лесоруб был тоже канадский, он решил рассчитаться с товарищами.
Со словами "вот моя доля" он достал восемь долларов.
Как двое лесорубов должны разделить деньги?
(считаем, что пироги одинаковы и съели все поровну).

16. Про вагоны

Есть состав из n вагонов, замкнутый в кольцо (т.е. первый соединен с последним). В начальный момент в каждом вагоне случайно включен или выключен свет. Наша задача - находясь внутри состава и не выходя из него, сосчитать число вагонов в нем. Все, что мы можем делать - включать/выключать свет в них (т.е. ставить метки, оставлять вещи или бить стекла не можем).

17. Классика. Задача египетских жрецов

18. Простенькая задачка от моей дочери

У двух друзей есть слоеный (т.е. горизонтально резать нельзя) прямоугольный торт, из которого какой-то гад, к сожалению, уже вырезал (и съел) прямоугольный кусок. Ориентация и положение вырезанного куска могут быть совершенно произвольными. Как разделить оставшийся торт на две равные по объему части одним прямолинейным разрезом?

(на решение - 1 минута. Для шибко умных - задачу можно усложнить до торта и отверстия произвольной формы.)

19. Топологическая задача тоже от моей дочери (сложная)

К картине обоими концами прикреплена длинная веревка. Необходимо повесить картину на стену с помощью N гвоздей так, чтобы при вытаскивании любого гвоздя картина и веревка падали. Как это сделать?

Для N=1 ответ тривиален.

Сначала можно поискать решение для N=2, ззатем для N=3, затем попробовать обобщить для произвольного N.

20. План побега. Очень нетривиальная задачка.

Заяц оказался в центре круглого пруда, на берегу которого стоит Волк. Заяц хорошо плавает, а Волк плавать не умеет, но его скорость на берегу в четыре раза больше, чем у Зайца в воде. Если Заяц выберется на берег в точке, в которой нет Волка, то убежит, поскольку бегает он быстрее. Сможет ли Заяц спастись в этой ситуации?

Решение

21. Ещё задачка от моей дочери.

Живёт в горах некое племя, которое охраняет 20 горных источников.
Все источники пронумерованы от 1 до 20.
Вода в источниках ядовитая. Но без вкуса и запаха. Яд такой что выпил и через сутки ласты склеишь.
Но если в течение последующих суток выпить воды из источника с бОльшим номером, то яд нейтрализуется.
Напали на это племя злые враги и в битве отбили источник под номером 20 (у защитников нет к нему доступа). Остальные остались на нейтральной территории (доступ есть у обоих племён). Битва была столь кровопролитной, что вожди решили не продолжать войну, а устроить "дуель".
Договорились так, что каждое племя выставляет по бойцу. Каждый боец приносит один стакан воды. Они меняются стаканами и каждый этот стакан выпивает. Чей боец останется жив, то племя и победило.
Как защитникам победить захватчиков?

Примечание 1. Считаем захватчиков не очень умными.
Примечание 2. До и после "дуели" можно пить что угодно.
Примечание 3. В этих горах есть реки и ручьи с обычной водой.

22. Тривиальная школьная задачка.

Представим, что земля - идеальный шар. Его по экватору стянули стальным облучем. Потом обруч разрезали в вварили дополнительный кусок длиной 1 метр. Образовалась щель.
Вопрос - сможет ли в эту щель пролезть крыса?
Считаем, что радиус земли 6400 километров.

22.1. Чуть менее тривиальная задачка в ту же тему.

Земля - идеальный шар радиусом 6400 км. По экватору натягиваем нерастяжимую нить. Затем увеличиваем длину нити на 1 см. (Один сантиметр). Оттягиваем в одном месте эту нить. Сможет ли в образовавшуюся щель пролезть кошка?

23. Задачка от Льва Николаевича Толстого

Две крестьянки продавали на рынке яблоки. Одна продавала за 1 копейку 2 яблока, другая за 1 копейку 3 яблока.
Пока все понятно, кроме цен  
У каждой было по 30 яблок. Соответственно одна по итогам дня наторговала на 15 копеек, другая на 10 копеек.

Тут одна из них заболела. И попросила вторую продать её яблоки тоже.  Опять же по 30 яблок, в итоге 60 яблок у бабки.
Она решила так - 3 яблока за 1 копейку и 2 яблока за 1 копейку - это 5 яблок за 2 копейки.

Получилось у нее из 60 яблок 12 пятияблочных кучек. Каждую из них она продала за 2 копейки... И оп-те нате! На выходе 24 копейки всего! А когда по раздельности продавали - 25 копеек.
Где копейка, где, блин, копейка, я вас спрашиваю!? 

24. До кучи ещё задачка от Л.Н.Толстого

Скорняк торгует шапками. Каждая шапка стоит 10 рублей. Утро, подходит покупатель и хочет купить шапку. Даёт 25-рублёвую купюру. У продавца нет сдачи. Он зовёт мальчишку-уборщика, даёт ему 25-рублёвку и отправляет к зеленщице разменять. Пацан меняет купюру, скорняк отдаёт покупателю шапку и 15 рублей сдачи. Покупатель уходит.
Через некоторое время прибегает зеленщица, показывает 25-рублёвую купюру и говорит, что она фальшивая. Скорняк внимательно еразглядыват купюру и соглашается - фальшивая. Что делать? Отдаёт зеленщице 25 рублей.

Вопрос - какой убыток понёс скорняк?

25. Задача юридически-математическая

Значит так.
Собрался один древний римлян помирать. Решил завещание делать. У него жена как раз в то время беременная была, так решил он и об жене и об ребенке позаботится. Указал так - если родится сын - 2/3 наследства ему, а жене 1/3.
Если же родится дочка - то дочке 1/3 наследства, а жене 2/3.

Указал, да и помер.

А жена возьми да и роди близнецов, причем мальчика и девочку. Вот и сели все на попу. Как делить?

26. Ещё одна подобная

У одного бедуина было 3 сына. Умирая, он оставил им в наследство 17 верблюдов, велев поделить так: старшему -- 1/2, среднему -- 1/3, младшему -- 1/9. Стали они делить, да как ни пробовали -- не смогли. Тогда решили они позвать дядю. Тот приехал к ним и разделил так, что все остались довольны. каким образом он это сделал?

27. Арифметическая.

Найти два числа так, чтобы их умножение, деление и сложение давали один и тот же результат.

Решение

28. Ещё арифметическая

Доказать что если взять любое простое число больше 3, возвести в квадрат и вычесть 1, результат будет всегда делится на 24.

29. Задачка по радиоэлектронике

Вспомнилась задачка с первого курса по радиоэлектронике. Точную постановку не помню, поэтому пришлось придумывать её заново.

Имеется схема из пяти сопротивлений, источника питания и вольтметра.
Найти показания вольтметра при напряжении, поданном на вход  U=12V.

30. В ту же тему, что предыдущая

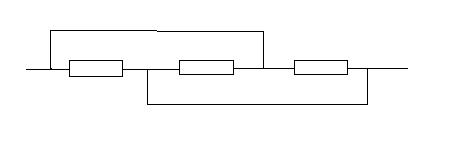
Каждый резистор по 1 килоому. Найти сопротивление цепи.

32. Ещё подобная задача. Популярна уже лет сто...

Есть проволочный куб. Сопротивление каждого ребра равно R, к противоположным вершинам приложено напряжение U. Найти сопротивление куба.

33. Ещё арифметическая

Бедуин продавал скот (верблюдов, лошадей и баранов). Всего он продал 100 животных и выручил за них 100 сиклей серебра. Причем верблюдов он продавал по 10 сиклей серебра за голову, лошадей по 3 сикля, а баранов по полсикля серебра. Спрашивается, сколько он продал верблюдов, сколько лошадей и сколько баранов, если известно, что он продал по крайней мере по одной штуке каждого животного.

34. Задачка за мой 7 класс. Но из категории "повышенной сложности"

Дано: (a-b)²=a²-2ab+b²
Доказать, что 2*2=5.
Доказательство:
   -20=-20 очевидно.
   16-36=25-45 очевидно.
   16-36+81/4=25-45+81/4
   4²-2*4*(9/2)+(9/2)²=5²-2*5*(9/2)+(9/2)²
   (4-9/2)²=(5-9/2)²
   4-9/2=5-9/2
   4=5
   4=2*2, следовательно
   2*2=5
Что и требовалось доказать :-)

35. Не люблю подобные задачи, но пусть будет. Головоломка для пиратов.

И.Стюарт

Десять пиратов получили в свои руки 100 золотых монет.
Теперь они хотят поделить награбленное.
Они действуют по правилам (это своего рода пираты-демократы). Самый свирепый пират предлагает, как разделить золото, а потом все,
в том числе и предложивший, голосуют “за’’ или “против’’ этого предложения.
Если 50 процентов или более пиратов согласны с предложением,
то оно принимается, и именно так и происходит дележка.
В противном случае предложившего выбрасывают за борт,
и новое предложение делает самый свирепый из оставшихся пиратов.
Все пираты с удовольствием выбросят за борт одного из своих товарищей,
но при возможности выбора любой из них предпочтет этого не делать, а получить золото.
Разумеется, никому из них не хочется быть выброшенным за борт самому.
Все пираты умеют рассуждать логически и каждый из них знает, что все остальные умеют рассуждать.
Никакие два пирата не равны по своей свирепости, таким образом,
они ранжируются в определенном порядке, который известен им всем.
Золотые монеты неделимы, и объединение пиратов для получения золота в целях последующего дележа его недопустимо, потому что пираты не доверяют друг другу.
Теперь вопрос: какое предложение должен внести самый свирепый пират,
чтобы получить как можно больше золота?

36. Задачка от Кенгуру для 8-го класса.

У Лёши часы забегают на 7 минут, а Лёша думает что они отстают на 8 минут. Лёша смотрит на часы и считает, что сейчас полдень. Сколько времени на самом деле?

37. Про царя и мудрых советников

У царя два мудрых советника. Он их вызывает и говорит. У меня есть белые  и чёрные колпаки. Завтра я надену на каждого из вас колпак и каждый увидит, какого цвета колпак на другом.
После того, как колпаки надеты, общаться запрещено.
Далее, я каждого спрошу, какого цвета колпак  надет на его голове. Ответ нужно написать.
Если хоть один ответит правильно, то я вас награжу, а если ни один не ответит правильно, то обоим головы отчекрыжу.
Что делать мудрецам?

38. Снова про царя и мудрых советников

Те два мудреца из предыдущей задачи остались живы и даже бабок подзаработали. Царь нанял ещё одного советника. Теперь их трое.
Царь их зовёт и говорит, - вот три чёрных колпака и два белых. Я сейчас надену на каждого по колпаку. По-прежнему, каждый видит колпаки на головах двух других и не видит, что на его собственной голове.
Советникам завязывают глаза и надевают колпаки. Снимают повязки. Советники задумываются.
Потом один говорит, - А! Я знаю, какого цвета на мне колпак.

Что он ответил и почему?

39. И третья задачка про мудрецов и злого царя.

Мудрецов уже стало 20.
Колпаки по-прежнему двух цветов - чёрные и белые.
Царь: завтра вам завяжут глаза, наденут, на головы колпаки, построят в колонну и снимут повязки. Первый не будет видеть никого. Второй будет видеть первого и колпак на нём.  Третий будет видеть двух первых, четвёртый - трёх первых и так далее. 20-й будет видеть всех 19 стоящих перед ним. В каком порядке их выстроят во время испытания, заранее не известно (жребий). Оглядываться нельзя.
Каждый из мудрецов в произвольном порядке может называть цвет колпака, который на нём надет. Если ответ неправильный, то голова того... нахрен.
Как мудрецы должны договориться между собой в этом случае?

40. Математик Колмогоров придумал эту задачу в 5 лет.

Есть пуговица с четырьмя дырочками.
Чтобы её пришить, достаточно протянуть нитку по крайней мере через две дырочки.
Сколькими способами можно это сделать?

(тут уже и у меня вопрос к Колмогорову. Если нитку протянуть из дырки 1 в дырку 2, эквивалентно ли это протягиванию нитки из дырки 2 в дыырку 1? Предлагаю считать, что нет. Ведь первый узелок будет у разных дырок :-)

41. Задача про стеклянные шарики.

Есть 100-этажный дом. Есть два идентичных стеклянных шарика. При падении с некоторого этажа шарики гарантированно разбиваются.
Определить минимальное число бросков шариков для выяснения этажа, при падении с которого шарик гарантированно разобьётся.
(в тырнеты не подсматривать).

42. Задачка от А.С.Чирцова.

Задачка взята из лекции А.С.Чирцова. Он преподаёт в Питерском ЛЭТИ.

У них была проблема с тем, что задачи на вступительные экзамены утекали ещё до начала экзамена. А вступительные экзамены проходили в Петергофе. Поэтому многие задания для вступительных экзаменов придумывались в электричке по дороге в Петергоф. Однажды Александр Сергеевич, будучи уже секретарём приёмной комиссии, приехал на экзамен прямо к самому началу. На доске уже были написаны задачи, а в аудитории сидело полно абитуриентов.

Он читает условие задачи и "зависает". Потом говрит другим преподам, - "э... ребята, у вас задача сформулирована некорректно", на что слышит, - "и этот купился!".

Когда он сказал, - "вы имели в виду что..?" и услышал ответ "да!", то заявил, - "так они ж не догадаются!", на что получил ответ, - "посмотрим". Чирцов заявил, что готов поспорить на бутылку шампанского, если догадается хоть один. В результате вынужден был поставить ящик - 6 бутылок. Всего было около 450 абитуриентов.

Итак, задачка:

На невесомой нерастяжимой нити длиной L прикреплён груз массой m. Нить свободным концом закреплена (например, на потолке).
В начальный момент времени t₀ нить натягивают (за груз) параллельно поверхности земли, то есть груз отводят на 90 градусов в сторону на длину нити L, и просто отпускают без придания ему какой-либо скорости.
В момент прохождения грузом вертикальной прямой, проходящей через точку подвеса, он имеет горизонтальную составляющую скорости - v_гор
Найти кинетическую энергию груза в этот момент (момент прохождения вертикальной прямой, проходящей через точку подвеса).
Сопротивлением воздуха можно пренебречь.

43. Задачка для устного счёта детей 5-15 лет от В.И. Арнольда

Из города А в город Б и из города Б в город А  на рассвете (одновременно)
вышли навстречу друг другу (по одной дороге) две старушки.
Они встретились в полдень, но не остановились, а каждая продолжала идти с той же скоростью, и первая пришла (в Б) в 4 часа дня, а вторая (в A) в 9 часов вечера.
В котором часу был в этот день рассвет?

44. Ещё из той же книжки В.И. Арнольда

На книжной полке рядом стоят два тома Пушкина: первый и второй.
Страницы каждого тома имеют суммарную толщину 2 см, а каждая обложка – 2 мм.
Червь прогрыз (перпендикулярно страницам) путь от первой страницы первого тома до последней страницы второго тома.
Вопрос: какой путь он прогрыз?

45. Элементарная задачка про три сейфа

В комнате три сейфа.  В одном из сейфов лежат два золотых слитка.
В другом сейфе хранятся два слитка серебра.
А в третьем сейфе находятся один слиток золота и один - серебра.
На каждом сейфе прикреплена табличка на которой указано, что находится в сейфе.
Но все таблички перепутаны, то есть в каждом из сейфов содержимое не соответствует тому, что написано на табличке.
Какое наименьшее количество слитков и из каких сейфов нужно достать не глядя, чтобы определить, как должны быть развешаны таблички на самом деле?

46. Задачка от физика Герцена Копылова из Дубны

Доказать, что произведение длин отрезков, соединяющих одну из вершин правильного N-угольника, вписанного в окружность единичного радиуса, со всеми другими вершинами равно N.

47. Задачка, которую мне подкинул парень из Железногорска по дороге на речку Урик

Сидят на пригорке кошка и обезьяна. Обезьяна спрашивает, - слушай, а у тебя есть дети?
Кошка, - да, трое.
Обезьяна, - а сколько им лет?
Кошка, - если перемножить их возраст, то будет 36, а если сложить... хм... будет количество окон вон в том доме.
Обезьяна, - ну.... я не знаю.
Кошка, - да, младший рыжий.
Обезьяна, - ну тогда всё понятно.

Сколько лет кошкиным детям?

48. Набор задачек, тоже подброшенный моей дочерью.

Это набор логических задач "Принцесса или тигр" придуманный Фрэнком Стоктоном.

Решать устно, в ответы не смотреть!

49. Совершенно феерическая задача, подсмотренная у Верта Дайдера.

В тюрьме находится 100 заключённых, которым присвоены номера от 1 до 100. Номера отпечатаны на тюремной робе.

Им устраивают следующее испытание:

Берётся 100 записок с номерами тоже от 1 до 100 и 100 коробок также пронумерованные от 1 до 100.

Записки с номерами случайным образом раскладываются в коробки по одной записке в каждую коробку.

Условие следующее:

Каждый заключённый входит в камеру с коробками и может открыть последовательно не более 50 коробок. Доставать записки из коробок нельзя. Переставлять коробки нельзя. Можно только открыть коробку, увидеть номер на записке и закрыть коробку. Задача - найти свой номер на записке. До начала испытания заключённые могут переговорить и выработать какую-либо тактику. После начала испытаний никаких переговоров нет. Просто испытуемого после прохождения отводят в другую камеру.

Если каждый из заключённых находит свой номер после открытия не более 50 коробок, то все 100 заключённых выходят на свободу, если же хоть один заключённый не находит за 50 открываний свой номер, то все 100 заключённых продолжают отсиживать свой срок.

Вопрос: какова вероятность выхода на свободу заключённых?

Решение можно посмотреть здесь, но сначала лучше понапрягать мозг.

50. Зеки и лампочка

Начальник тюрьмы собрал заключенных и говорит: "Сыграем в игру: сейчас вы посовещаетесь между собой, а потом вас разведут по одиночным камерам, и будут раз в день выбирать одного из вас и отводить ненадолго в комнату, где есть только одна лампочка и выключатель. Изначально лампочка выключена.

Во время нахождения в комнате можно включить выключенную лампочку, выключить включённую, или ничего не трогать.

Каждый из вас побывает в комнате с лампочкой и неоднократно.

Ваша задача такая - любой из вас зайдя в комнату может сказать охраннику "Я знаю, что в этой комнате побывали все". Если он оказывается прав, и в комнате с лампочкой к этому моменту действительно успел побывать каждый заключенный (хотя бы по разу), то вас всех освободят. Если он ошибётся, то расстреляют."

Какой алгоритм следует выработать зекам прежде чем их разведут по камерам (после этого они общаться уже не могут)?

51. Ещё одна задача от Верта Дайдера

Есть две окружности примерно такого вида:

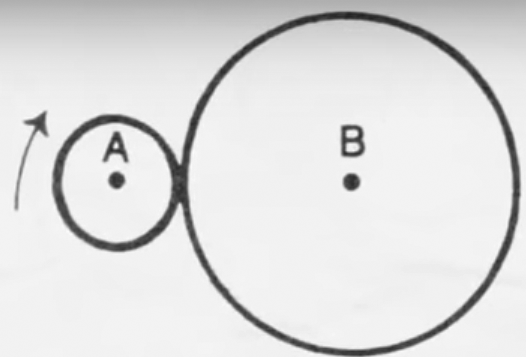
Радиус окружности А в три раза меньше радиуса окружности B. Окружность А катится вдоль неподвижной окружности B как показано на рисунке без "проскальзывания".

Сколько полных оборотов совершит окружность А для того, чтобы вернуться в исходное положение?

В общем виде эта задача рассмотрена здесь.

52. Задачка на сообразительность

Альпинист стоит на обрыве отвесной скалы высотой 100 метров. Рядом растут несколько деревьев. На середине отвесной скалы на высоте 50 метров есть небольшой уступ, на котором растёт дерево. У альпиниста есть верёвка длиной 75 метров. Как альпинисту спуститься вниз?

Подсказка - верёвку можно резать (поперёк) на любые куски.

53. Простенькая алгебраическая задачка

Дано: X² - X³ = 12

Найти X (желательно все значения, а не только очевидное)

Ответ здесь

Пока хватит. Будет ещё, но потом, может быть...

С уважением,
ваш Marksman